1. 상관분석
•
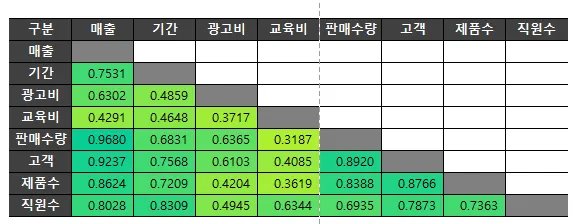
상관분석: 선형적 또는 비선형적 관계를 갖고있는지를 분석하는 방법
•
상관관계: 관계 있는지 아닌지 파악
•
상관계수
◦
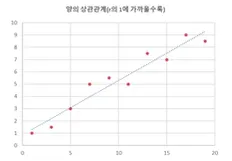
0.7이상이면 강한 양의 상관관계
◦
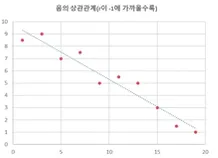
-0.7이하면 강한 음의 상관관계
→ 0이 상관관계가 없는 것이지, -1은 ‘강한 음의 상관관계’가 있다고 생각하면 됨
•
실습
◦
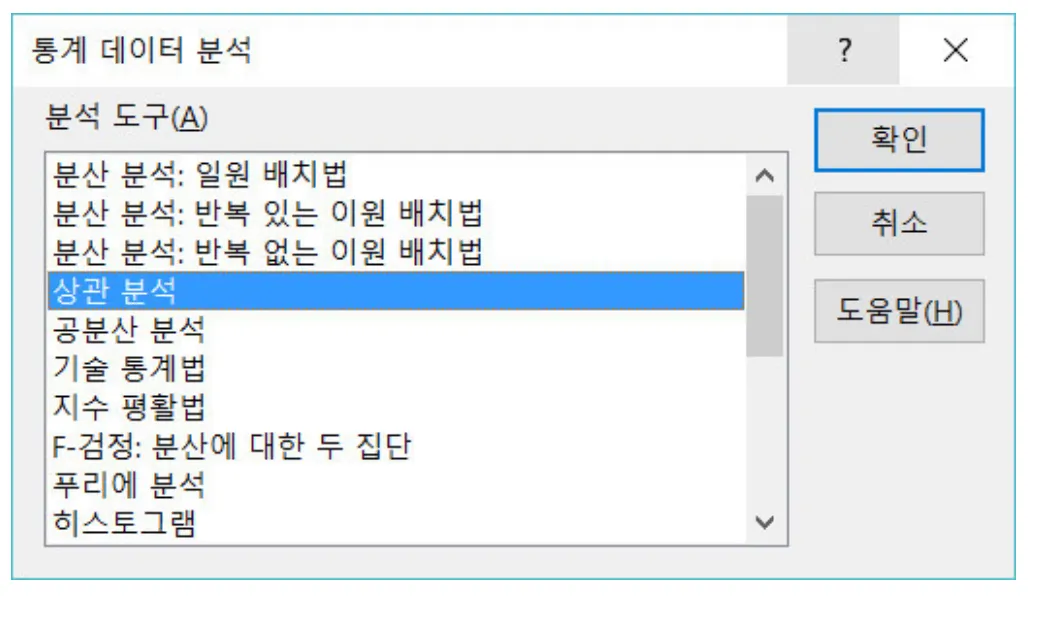
상관관계: 데이터분석 → 상관분석 → 분석하려는 데이터 범위 선택
◦
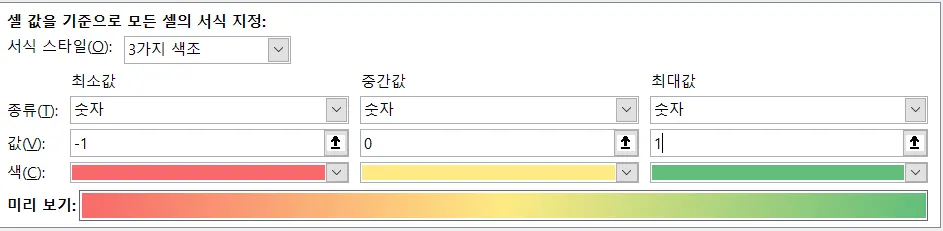
색조: 조건부 서식 → 새 규칙
▪
종류는 숫자로
▪
값 -1, 0, 1
2. 분산 분석의 이해와 활용
회귀분석은 인과관계를 비교, 분산 분석은 집단을 비교
회귀분석 → 매출을 종속변수라고 할때, 영향을 미치는 독립변수들(광고비, 교육비, 콘텐츠 등등)
분산분석 → 큰 틀, 예를 들어 페이스북/인스타그램에서의 결과를 기준으로
(그룹에 따라 어떤 효과가 존재한다는 점을 알려줄 뿐, 어떤 그룹이 구체적으로 어떻게 효과가
있는지는 말해주지 않는다)
일원독립 분산분석
•
분산 분석: 두 개 이상 다수의 집단을 비교해 평균의 차이가 있는지를 검정
•
분산 분석의 방법
◦
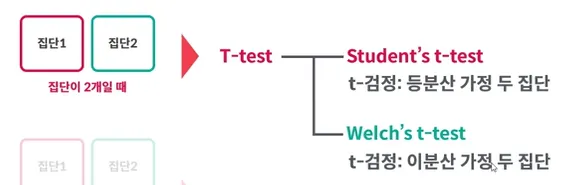
집단이 2개 일 때
◦
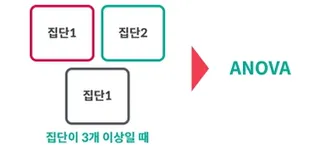
집단이 3개 이상일 때
•
1.
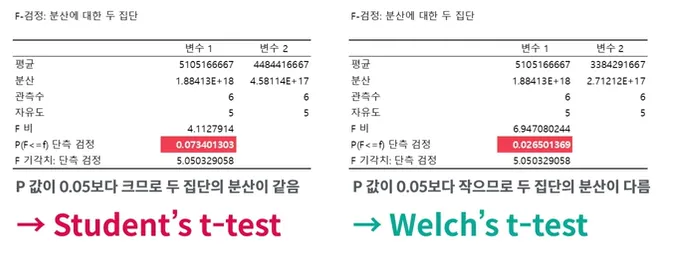
F - 검정
F - 검정은 두 집단의 등분산성을 검정해 각 상황에 맞는 T-Test방법을 선정하기 위해 사용. 방법을 선정하기 위해 사용!
•
P - value가 0.05보다 크면 두 집단의 분산은 같고,
•
0.05보다 작으면 두 집단의 분산은 다르다
◦
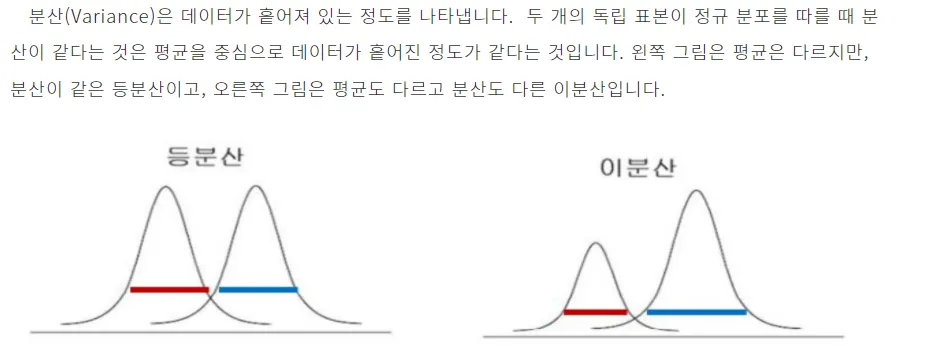
등분산성과 이분산성의 의미
→ 두 독립 표본이 같다는 것은 평균과 분산이 같다는 것을 의미
2.
T-Test 진행
•
P > 0.05 일때(등분산성 일때) → t - 검정: 등분산 가정 두 집단 사용
•
P < 0.05 0.05 일때(등분산성 일때) → t - 검정: 이분산 가정 두 집단 사용
•
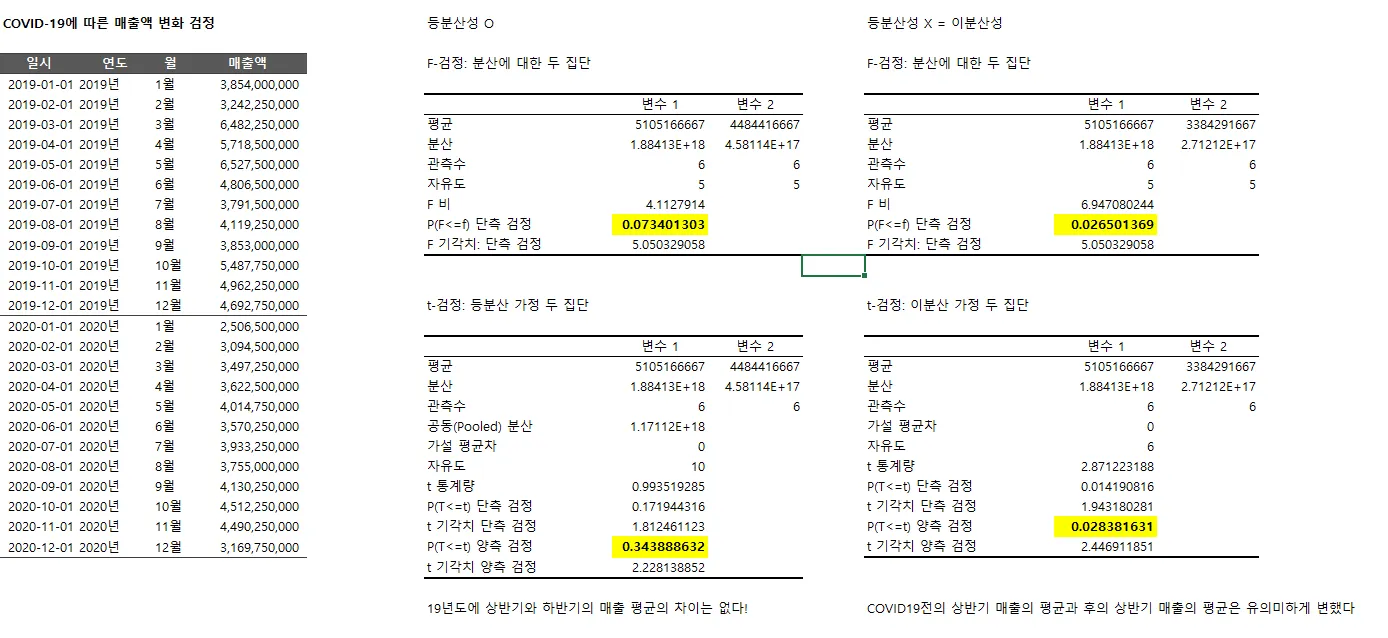
실습
◦
상반기와 하반기의 매출 평균의 차이는 별로 크지 않다
◦
covid19전 상반기의 매출 평균과, 이후 상반기의 매출평균은 유의미하게 변했다
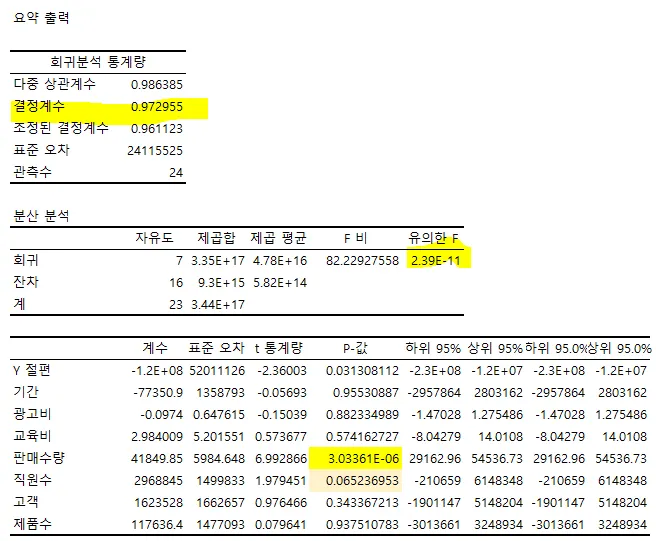
3. 회귀분석
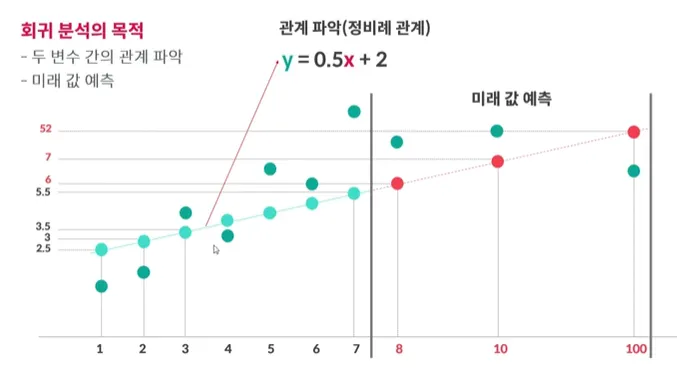
두 개 이상의 연속형 변수 (수치)인 종속 변수와 독립 변수 간의 관계를 파악하는 분석
(ex. 광고비 투입에 따른 매출 변화, 저번에 이정도 광고비에 이정도 매출을 냈으니까 이번에도 이정도 나오겠네? 예측 가능)
→ 두 변수 간의 관계 파악
→ 미래 값 예측
•
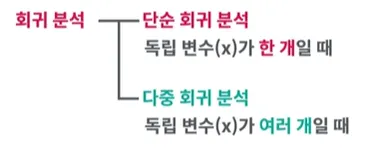
회귀 분석의 종류
◦
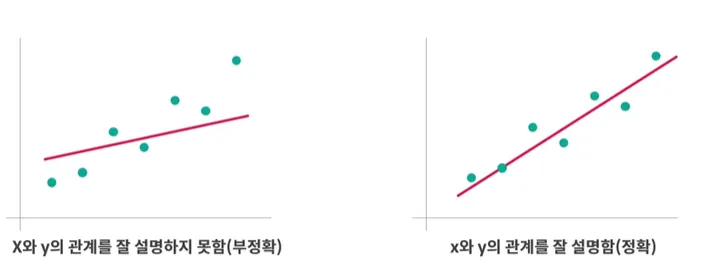
결정계수 → R스퀘어
0~1값을 가짐. 1에 가까울 수록 회귀 모형이 실제 값을 잘 설명함
(0.937이면 93.7%를 설명할 수 있다는 뜻)
◦
조정된 결졍계수
결정계수의 경우 독립변수의 개수가 증가하면 일방적으로 증가하는 경향이 있음. 이를 보완하기위해 조정된 결정계수는 독립변수가 증가할 때 분자를 감소시켜주는 연산을 통해 일방적인 증가를 방지
◦
유의한 F
▪
0.05미만이면 → 대립가설을 채택 → 회귀계수가 0이 아니다 → 독립변수들 중 적어도 하나 이상의 변수가 종속변수를 설명함에 있어 유의하다 이 회귀 모형이 유의미하므로 사용 가능
▪
0.05 이상이면 → 귀무가설을 채택 → 이 독립변수는 종속변수에 영향을 미치지 않는다
◦
회귀식
y = ax+b 에서 Y절편은 b값을, X1 값은 a(기울기)를 뜻함
(ex. Y절편이 -4.E+07, X1이 56081이면, 회귀 모형식은 y=56081x-4.E+07
x에 광고비를 넣으면 y 매출이 나오는..)
◦
P 값
▪
F값에 대한 유의확률을 의미 → 0.05 보다 작으면 회귀모형에 적합
(유의확률: 이 값이 0.01보다 작은 값이면 99%의 신뢰구간에서 유의하다는 것을 의미함
0.05보다 작은 값이면 95%의 신뢰구간에서 유의하다는 것을 의미.
그 변수가 종속변수에 유의한 영향을 미친다 )
3-1. 단순 회귀 분석
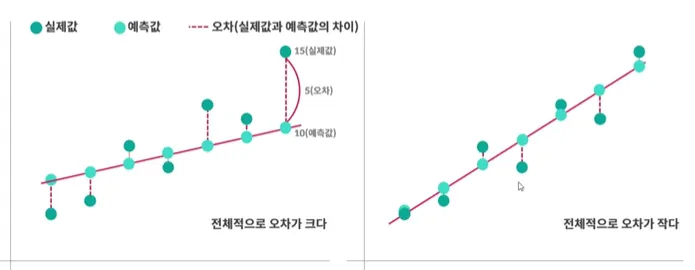
독립 변수(x)가 변할 때, 종속 변수(y)값이 어떻게 변하는지를 가장 잘 설명해주는 직선을 찾아 분석하는 방법 → 직선을 그려내는 것!
‘최소 제곱법’으로 전체적으로 오차가 작은 직선을 찾는다
•
실습
◦
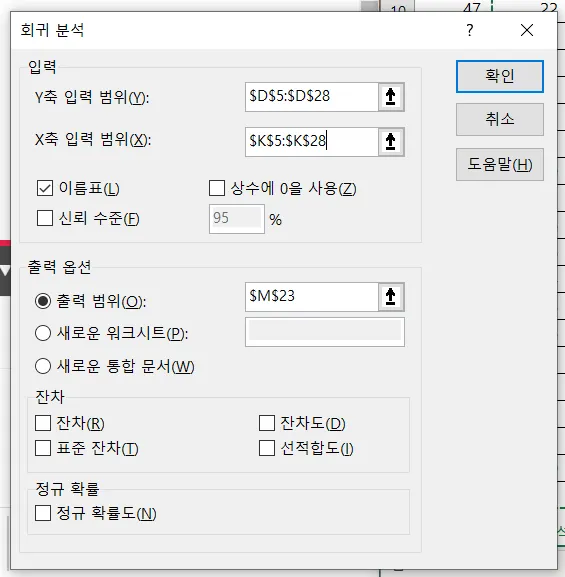
데이터 → 데이터분석 → 회귀분석
▪
Y축은 매출, X축은 직원 수 → 직원수의 변화에 따른 매출의 변화
▪
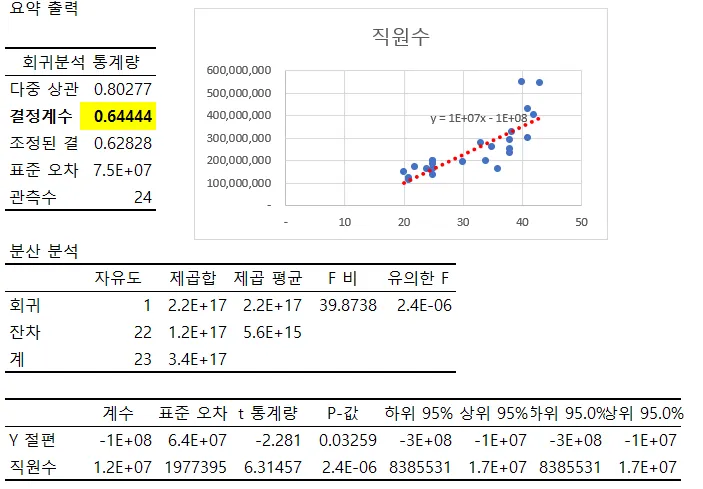
결정계수를 보니 64%밖에 설명을 못하고 있음
▪
선점도 그래프도 오른쪽에 그려줌 → 추세선 추가, 공식추가(저 공식 안에 X,값을 넣으면 Y값이 나온다는 뜻)
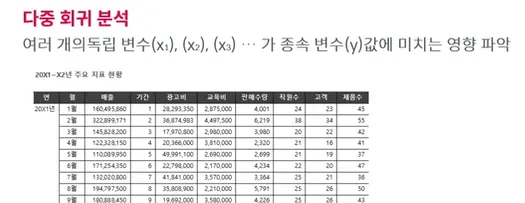
3-2. 다중 회귀 분석
여러개의 독립변수로 분석
•
다중 회귀 분석의 평가와 해석
◦
조정된 결정 계수
◦
유의한 F
독립변수 중 적어도 하나 정도는 종속변수를 설명하기에 있어서 유의하다
◦
P값
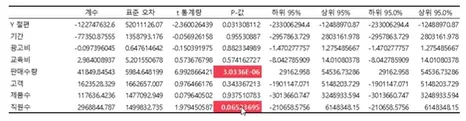
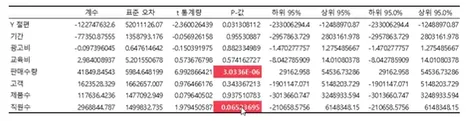
P값이 0.05이하인 변수들이 종속 변수 y(매출)을 가장 잘 설명하는 변수들
ex) 직원 수는 0.05보다 크지만, 거의 0.05에 가까우므로 직원수가 많아지면 0.05 미만이 될 가능성이 큼
•
실습
◦
판매수량과 직원수가 의미 있는 데이터를 보임
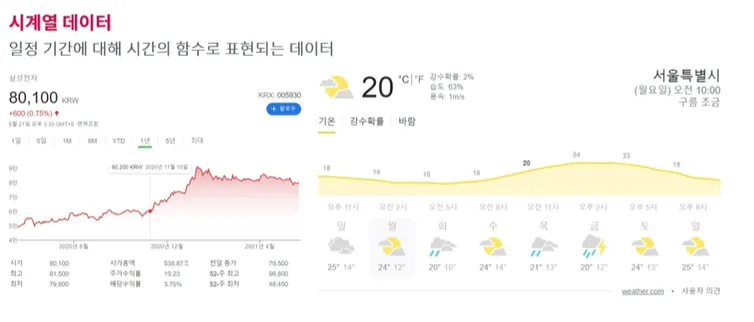
4. 시계열 데이터
일정 기간에 대해 시간의 함수로 표현되는 데이터
→ 과거 시계열 데이터 특성 파악 및 미래 데이터 예측 업무(흐름이 있는 데이터)
•
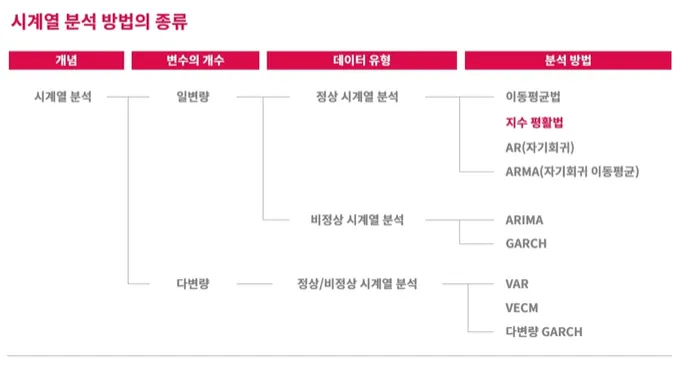
시계열 분석 방법의 종류
◦
일변량
→ 시간의 흐름에 따른 온도의 변화만 보겠다 이런 것들
◦
다변량: 대부분 비정상 시계열 데이터인데, 불규칙성을 유발하는 요소들을 제거하고 정상 시계열로 만들어서 볼 수 있음
▪
정상 시계열 분석
▪
비정상 시계열 분석
4-1. 지수평활법
•
현재의 실제 값과 현재의 예측값을 합산하여 미래의 예측 값을 구하는 방법