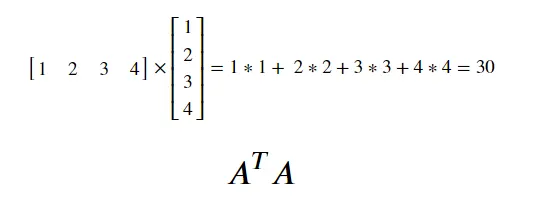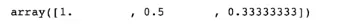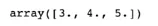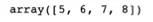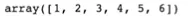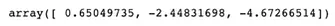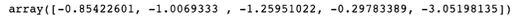CHAPTER 4-1. Numpy
1. Numpy란
•
numpy: numerical python
◦
numerical computing: 컴퓨터가 실수값을 효과적으로 계산할 수 있도록 하는 연구 분야
◦
vector arithmetic: 벡터 연산 → 데이터가 벡터로 표현되기 때문
•
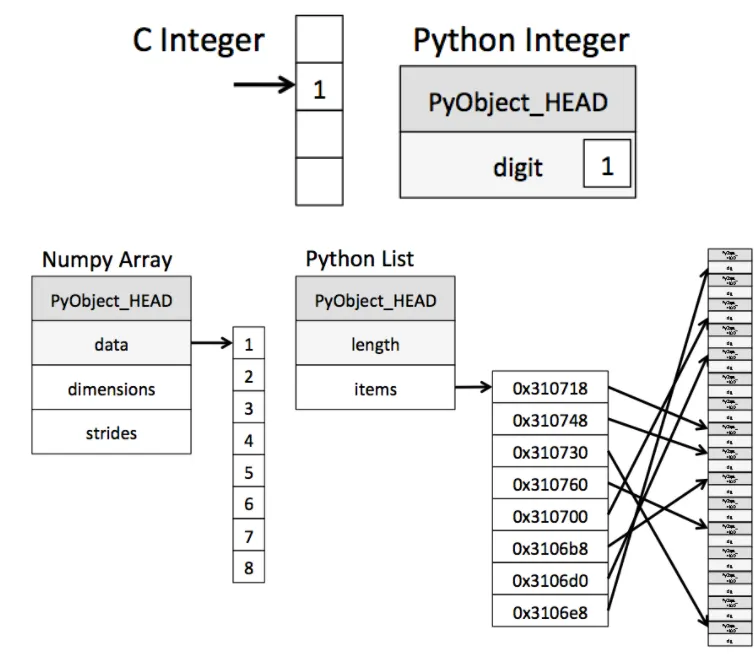
numpy array >> python list(or tuple) 성능이 더 뛰어남
◦
python list와 비슷한 개념을 numpy에서는 numpy array라고 부름
→ 파이썬 리스트처럼 여러 데이터를 한번에 다룰 수 있으나, 모든 데이터가 동일한 data type을 가져야합니다.
•
numpy array는 만들어지고 나면 원소의 update는 가능하지만, array의 크기를 변경할 수는 없음
→ append라는 함수가 있으나, 의미가 다름
2. 데이터 분석을 위한 선형대수학
•
구분
◦
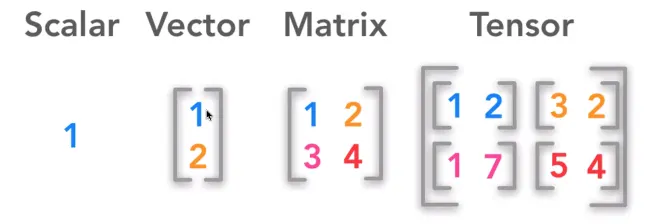
scalar: 한개의 숫자
◦
vector: 리스트와 같은 유형 → 크기와 방향이 있음
문자의 경우도 왼쪽에서 오른쪽으로 읽는 특성이 있기 때문에 vector 데이터라고 함
◦
Matrix: 행렬데이터 (e.g 엑셀)
◦
Tensor: 메트릭스에서 축이 하나 늘어나게 되면 3차원이 됨 (e.g. 이미지, 동영상)
•
데이터분석에 자주 사용하는 특수한 연산 → 벡터와 벡터의 내적
◦
내적이 이루어지려면
▪
벡터가 마주하는 shape의 갯수(길이)가 같아야 합니다.
e.g (1,4)와 (4,1)→ (1,1) / (3,5)와 (5,4) → (3,4)
▪
연산 앞에 위치한 벡터는 전치(transpose) 되어야 합니다.
CHAPTER 4-2~3. Array
1. Array 만들어보기
•
불러오기: import numpy as np
•
파이썬 리스트 선언
◦
1차원: data = [1, 2, 3, 4, 5]
◦
2차원
•
numpy array를 만들기 → 파이썬 list를 numpy로 변환하는 것
◦
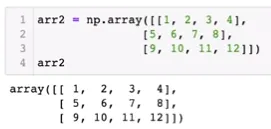
생성하기: arr2= np.array(data) → arr2 = np.array([1,2,3,4,5]) 동일
◦
크기확인 :arr2.shape = (3,3) → 3 x 3 이라는 뜻
◦
차원확인 : arr2.ndim = 2 → 2차원이라는 뜻
◦
크기 : arr2.size = 9 → 말그대로 곱하기임
◦
타입확인 : arr2.dtype = int 64 → 원소의 타입 integer + 64 bits
◦
공간: arr2.itemsize = 8 → 바이트
2. Array Initialization
•
공간을 만들어주는 작업
◦
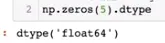
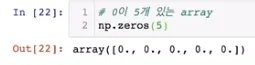
원소가 0인 array를 생성하는 np.zeros()
▪
np_zeros의 디폴트갑 : float64
▪
0이 5개 있는 array
▪
0이 3x3인 array
튜플로 넘겨줘야함
◦
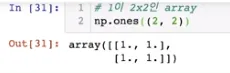
원소가 1인 array를 생성하는 np.ones()
▪
1인 3개 있는 array
▪
1이 2x2인 array
◦
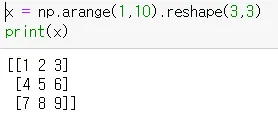
특정 범위의 원소를 가지는 np.arange()
→ range의 경우에는 그 자체로는 그냥 범위인데
arange는 바로 일렬로 만들어줌
3. Array Operation
•
numpy array를 쓰는 가장 큰 이유는 vector처럼 사용할 수 있기 때문
e.g. arr1 = np.array([1, 2, 3, 4, 5]) --> (1, 2, 3, 4, 5) # vector
•
그렇기 때문에 scipy, matplotlib, scikit-learn, pandas, tensorflow, pytorch 등 대부분의 데이터분석 라이브러리들이 numpy array를 사용
•
vector와 tuple 비교
→ vector는 원소끼리의 수가 동일해야 함
◦
tuple addition
◦
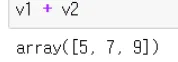
vector addition
◦
vector @ → 각각의 위치에있는 원소를 곱해서 더한것
v1 @ v2 = 32
1x4 + 2x5 + 3x6
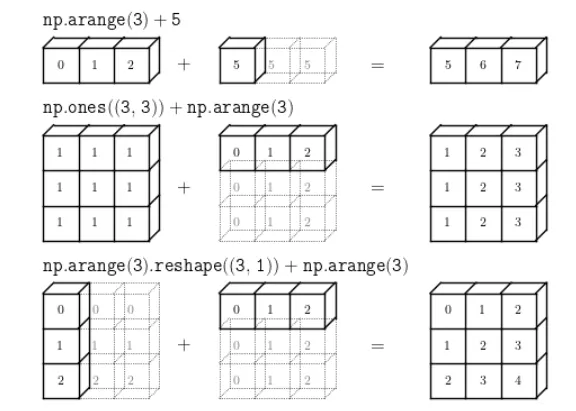
4. Broadcast
•
서로 크기가 다른 numpy array를 연산할 때, 자동으로 연산을 전파(broadcast)해주는 기능
•
예제
◦
더하기와 곱하기
5. Universal Functions
•
numpy array는 하나의 함수를 모든 원소에 자동으로 적용해줌
•
int → float 변경하기
◦
arr1 = np.array([1,2,3] , dtype = float)
◦
arr1 / 1 → 나누기를 할 때 자동적으로 float으로 바꾸기 떄문에
•
모든 원소를 역수를 취하기
◦
1/arr1
arr1 = np.array([1,2,3])
•
모든 원소에 2를 더할 때
◦
arr1 + 2
•
array 연산
◦
행렬 내적
test_array @ test_array.T 값: 30
내적은 어떨때 사용하나?
예: 쇼핑을 할 때 각 물건의 가격은 데이터 벡터, 각 물건의 수량은 가중치로 생각하여 내적을 구하면 총금액을 계산할 수 있습니다.
•
예제
◦
포트폴리오
# 각 종목의 가격은 80,000원, 270,000원, 160,000원이다.
# 삼성전자 100주, 셀트리온 30주, 카카오 50주로 구성하기 위한 매수금액을 구하시오
# (80000 * 100) + (270000 * 30) + (160000 * 50)
price = np.array([80000, 270000,160000])
stock = np.array([100, 30, 50])
price @ stock
2410000
Python
복사
◦
취향 비교
▪
v1과의 내적 구하기: v1 @ v2 = 1 , v1 @ v 3 = 2 ...
→ 내적의 크기가 클 수록 v1과 취향이 겹침
→ v3, v5, v6가 본것들 중 그 사이에서 내적이 큰 것들을 v1에게 추천
도깨비와 지옥을 추천해주는데 도깨비가 취향이 더 클 확률이 큼
▪
v2과의 내적 구하기: v2 @ v1 = 1 ... v2 @ v6 = 2
→ v6과의 내적이 가장 크기때문에 v6이 본것중 v2가 안본것들을 추천
오징어게임과 도깨비를 추천
CHAPTER 4-4. Array Indexing
1. Indexing
•
1차원 일 때
◦
arr1 생성 arr1 = np.aragne(10)
◦
인덱싱 arr1 [ 0 ]
◦
슬라이싱 arr1[:3]
array([0,1,2])
•
2차원 일 때
◦
arr2의 2, 3 원소 → 7 arr2[1][2] = arr2[1,2]
리스트와는 다르게 인덱싱 안에는 숫자들을 넣을 수 있음
◦
arr2의 세번째 컬럼 (3,7,11) arr2[:, 2]
→ arr2에 있는 모든 row에 대해서 세번 째 원소를 indexing
arr2(0,2)
arr2(1,2)
arr2(2,2)
arr2에 있는 모든 원소에 대해 세번째 인덱스를 쓰겠다
◦
arr2의 두번째 row arr2[1] = arr2[1, :]
→ arr2에 있는 두번째 row에 대해서 모든 원소를 indexing
2. Masking
•
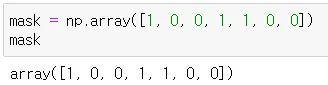
기본 array에 마스크 만들기
◦
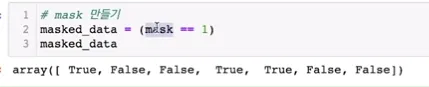
numpy인 mask가 1인 원소들
◦
mask에서 1인 원소일 때만 true가 나옴
•
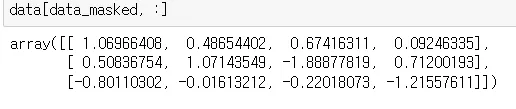
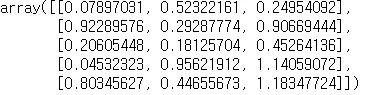
랭덤으로 생성한 data에 mask적용
◦
masked_data에서 true가 나온 row만 추출 → 1, 4, 5
위의 절차를 생략하고, data[mask == 1, :] 로 바로 생성 가능 → fancy indexing
•
fancy indexing
◦
data[ : , 0] < 0 → 첫 번째 column의 값들 중 0보다 작은 것
◦
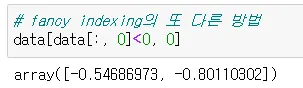
data [data[ : , 0] < 0, 0 ] data에서 0 보다 작은 column이 있는 행에서 첫 번째 원소
◦
data [data[ : , 0] < 0, 0 ] = 0
data에서 0 보다 작은 column이 있는 행에서 첫 번째 원소를 0으로 치환
◦
data[data < 0] = 0 모든 데이터를 대상으로 했을 때 0보다 작은 것들을 0으로 치환
CHAPTER 4-5. Array Functions
1. Numpy Methods 유용한 넘파이 함수들
•
np.random.randn(5,3) → random sampling을 한 원소를 가지는 5x3행렬을 만든다
•
np.abs(mat1) → 절대값 씌우기
•
np.square(mat1) → 제곱
•
np.sign(mat1) → 부호
•
np.floor(mat1) → 내림
2. Reshaping Array
•
reshape(x,y) → 행렬의 shape을 변경하기
3. concatenation or arrays
•
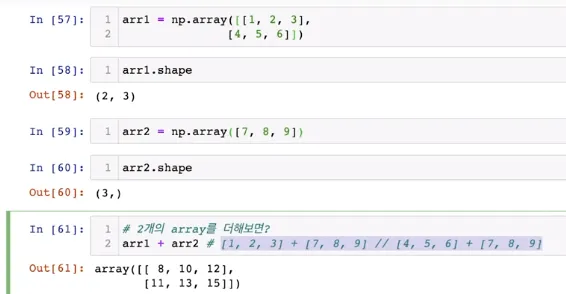
arr1 + arr2 를 하는 경우 → 각 벡터를 더함
•
np.concatenate([arr1, arr2]) → 두개의 벡터를 합치는 것
arr1, arr2를 리스트로 만들어서 합치는 것
•
np.vstack([arr1, arr2]) → vertically 쌓는 것
•
np.hstack([arr1, arr2]) → horizantally 쌓는 것
CHAPTER 4-6. Aggregation Functions
•
•
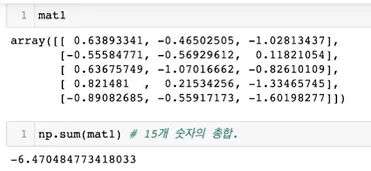
np.sum(mat1) → 모든 원소를 다 더한 값
◦
np.sum(mat1, axis = 0) 컬럼별 총합
◦
np.sum(mat1, axis = 1) 로우별 총합
•
np.sort(mat3, axis = 0) 정렬
•
np.argmin(mat3, axis =0) 최소값이 있는 인덱스